ELSIの我がグループ「前生物化学グループ」は、アミノ酸、ヌクレオチド、およびそのポリマーといった生命の成分を非生物的に合成しようとしている。この試みは重要である。なぜなら、原始地球に生命が誕生した環境条件を推定する方法として、考えられる道の一つであるからである。しかし、たとえ私たちが生命のこれらの構成要素を合成することに成功したとしても、それ自体では生命を生み出さない。生命は構成要素の合成のみならず、システムなのだ。より正確に言えば、生命は全体（システム）がその部分（構成要素）の合計よりも大きい何かである複雑なシステムであり、全体の利益と部分の利益の相反について考えなければならないことを意味する。

この点で、「渋滞ゲーム[2]」と呼ばれるアルゴリズムゲーム理論[1]の抽象的な問題は、私が「部分－全体」の相反する関係を考えるきっかけとなった[3]。

渋滞ゲーム理論は、活性物質にたとえられる。つまりそれぞれが自分の利益を追求するための知的能力を持っている。

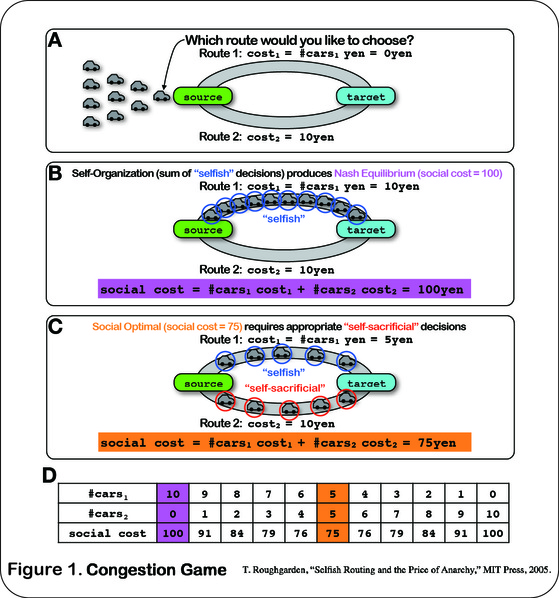
図1Aの概略図にあるように、「出発点の」都市から「目的地の」都市に移動するために10台の車が2つのルートを選べる状況を想像してみよう。ルート1をとる場合のコスト（通行料）は、その時点のルート1上の車両の数によって変化する。たとえば、ルート1に5台の車がある場合は、5円となる。一方、ルート2の通行料は常に10円に設定されている。あなたが車の運転手だったとする。どちらのルートを選択するだろうか？

最初の車（グループの頭）のドライバーは、ルート2が10円であるのに対し、無料（0円）のルート1を確実に選択する。 2人目の運転手も十分利己的なので、ルート1をとる。なぜなら費用は1円しかかからず、10円よりもずっと安いからだ。残りの運転手も、自分の利益を追求するという利己的な決断を下すだろう。 10台目の車も10円ではなく9円を支払う方を選ぶ。もしルート1を抜けるのに相当な時間がかかるとしたら、図1Bに示すように、最終的にはルート1にすべての車が集中する状況を作り出す。

では、このシステムですべての車が支払った総費用である「社会的費用」を考えてみよう。図1Bの状況では、すべての車が最終的に10円を支払うことになるため、社会的費用は100円になる。結局システムにとって最も損失をまねくことが判明した。社会的費用を最小限に抑えたい場合は、図1Cに示すように、コストの高いルート2でも5台の車を割り当てるのが最適だ。図1Dは、関数として変化する、車割当てパターンの考え得るすべての社会的費用を表している。図1Bおよび図1Cで説明した状況が、それぞれ最大および最小システム負荷となることがわかる。

これによりわかることは、上記のようなシステムでは、構成要素の利益を追求する利己的な行動の累積がシステムの利益を大きく失うことを示している。言い換えれば、この設定では、構成要素がチームとして働くことができれば、大きな利益を得ることができる。適切な比率の構成要素がコストの高いオプションを選択すると、システムによって支払われる社会的負担が最適になる。 「社会的最適」（図1C）は、中央政府のような一種の「トップダウン」制御装置を組み込み、費用のかかるルートを選択するように構成要素の一部に指令を出すことで達成できる。

しかし、私は社会的最適を「ボトムアップ」で達成する可能性に注目している。トップダウン制御が存在しない場合でも、ドライバーが、一種の通信チャンネルを使用して互いに対話することが許されていれば、チームとして社会的に最適な決定を下すことができる。できるだけ低い料金を保つことを望むルート1を走るドライバーの中には、残りのドライバーが入ってくるのを拒否し、彼らに不本意ながらルート2を選ばせるかもしれない。あるいは、交通混雑を減らすことを期待して、「自己犠牲」の精神で自発的にルート2を選ぶドライバーもいるだろう。そして、それが強制的に行われたのか、自発的に行われたのかにかかわらず、相互作用を通じて、適切な数の車がコスト高の選択をする可能性がある。

ここで、前生物化学の話に戻ろう。私は上記の観察が生命の起源時に存在していた前生物分子に適用できるかどうかに興味がある。この比較をするにはいくつかの飛躍があることに気が付く。もちろん分子には知的能力はないが、エネルギー、安定性、堅牢性などの観点から自らの利益を追求することができるだろう。たとえ分子がそれ自身で社会的に最適な決定を下すことができなくても、周囲の環境によって互いに相互作用し、システムのほぼ最適な状態をもたらすことができる。分子間の相互作用のいくつかのパラメータを含むこのような環境は静的であってはならず、分子の状態に応じてその条件を動的に変える必要があるかもしれない。私は特定のダイナミックな環境の下で分子がそのようなシステムを構成することによって大きな利益を得るのではないかと想像し、多様な環境が提供される原始地球で生命が出現した理由の1つではないかと考えている。

どうすればそれが可能になるか？これは、複雑な化学反応ネットワーク[4]における創発現象を探究する「システム化学」と呼ばれる新しい分野が対象とする研究課題である。この質問に答えることができなければ、初期の生命を支えていた非常に重要な化学システムの性質を理解することはできない。単純な分子集合の段階から複雑な分子ネットワークの段階への移行を引き起こすいくつかの必要性があったに違いない。

私は、分子が利己的な判断をしながら、好ましくない均一のとれた状態に落ち着くことで、チームとして働くシステムを構成するときに大きな利益を得ることができるという、上述の状況を表現する化学実験をデザインしたいと考えている。この実験が成功すれば、生命の起源を支える分子の環境条件を理解するための多くの手掛かりを生み出すと信じている。そのような実験をどのようにデザインするかについて意見があれば、共有してもらいたい！

文献

[1] N. Nisan, T. Roughgarden, E. Tardos, E, V. V. Vazirani (eds.): Algorithmic Game Theory. Cambridge University Press (2007).

[2] T. Roughgarden: Selfish Routing and the Price of Anarchy. The MIT Press (2005).

[3] M. Aono, Y. Hirata, M. Hara, K. Aihara: Greedy versus social: Resource-competing oscillator network as a model of amoeba-based neurocomputer, Natural Computing 10, 1219-1244 (2011).

[4] http://www.jsystchem.com/

References

[1] N. Nisan, T. Roughgarden, E. Tardos, E, V. V. Vazirani (eds.): Algorithmic Game Theory. Cambridge University Press (2007).

[2] T. Roughgarden: Selfish Routing and the Price of Anarchy. The MIT Press (2005).

[3] M. Aono, Y. Hirata, M. Hara, K. Aihara: Greedy versus social: Resource-competing oscillator network as a model of amoeba-based neurocomputer, Natural Computing 10, 1219-1244 (2011).

[4] http://www.jsystchem.com/