Our group at ELSI, the prebiotic chemistry group, is trying to synthesize abiotically the components of life, like amino acids, nucleotides, and their polymers. This attempt is important because it is one of the conceivable paths to estimate the environmental conditions for which life has emerged on the primordial Earth. But even if we succeed in synthesizing those components of life, that in itself does not make life. Life is a system, not just the gathering of the components. More precisely, life must be a complex system such that the whole (system) is something greater than the sum of its parts (components), implying that we should think about conflicts between the interests of the whole and that of the parts.

In this respect, an abstract problem from algorithmic game theory [1], called the Congestion Game [2], inspired me to consider the conflicted part-whole relation [3].

Congestion Game theory applies to active agents, each of whom has an intellectual capacity for pursuing its own interest.

Let us imagine a situation in which there are two routes for ten cars to move from the "source" city to "target" city, as drawn schematically in Fig. 1A. The cost (toll) for taking route 1 varies as a function of the number of the cars on route 1 at the time; for example, if there are five cars on route 1, then it costs 5yen. On the other hand, the toll of route 2 is set at 10yen constantly. Suppose you were a driver of one of the cars. Which route would you like to choose?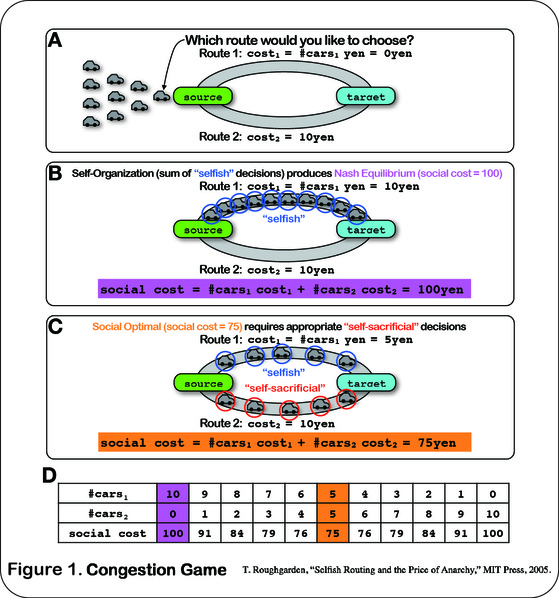


The driver of the first car (the head of the group) will definitely choose route 1 because it is free (0yen) whereas route 2 costs 10yen. The second driver will also be selfish enough to prefer route 1 because it costs only 1yen, much cheaper than 10yen. The same goes for rest of the drivers as they will make selfish decision to pursue each of their own interest; even for the tenth car, the driver will like to pay 9yen rather than 10yen. Finally, it will create a situation in which route 1 is occupied by all the cars as shown in Fig. 1B, if it takes a sufficiently long time to pass through route 1.

At this moment, let us consider the "social cost", which is the total cost paid by all the cars in this system. In the situation shown in Fig. 1B, the social cost becomes 100yen because every car should pay 10yen at the end. However, it turns out that this situation causes the heaviest loss for the system. If one wishes to minimize the social cost, it is optimal to allocate five cars even on costly route 2, as shown in Fig. 1C. Fig. 1D shows all possible amounts of the social cost that varies as a function of the car allocation pattern; it indicates that the situations described in Figs. 1B and C produce the maximal and minimal system burdens, respectively.

These observations tell us that, in a certain class of systems as described above, the accumulation of selfish behavior to pursue the interests of components results in the great loss of the interest of the system. In other words, under this setting, the components can obtain a great benefit if they could work as a team; when some of the components at the appropriate ratio choose the costly option, the social burden paid by the system becomes optimal. The "social optimal" (Fig. 1C) could be achieved when the system incorporates a kind of "top-down" control unit like a central government that instructs some of the components to choose the costly route.

However, I am interested in the possibility to achieve the social optimal in a "bottom-up" manner. Even in the absence of the top-down control, the drivers may be able to make the socially optimal decision as a team, if they were allowed to use some communication channels to interact with each other. Some drivers on route 1 who wish to keep the toll as low as possible may refuse to allow the rest of the drivers to come and may lead them to choose route 2 unwillingly. Or, some drivers may choose route 2 willingly with a spirit of "self-sacrifice", expecting to reduce traffic congestion. Then, there are some possibilities that an appropriate number of the cars can make the costly decision through the interaction, regardless of whether it was made mandatorily or spontaneously.

Now, let us come back to the discussion on prebiotic chemistry. I am interested in whether the above observations could be applied to the prebiotic molecules that were present at the origins of life. I realize that there seems to be some jumps for making this comparison. Of course the molecules would have no intellectual capacity, but they would be capable of pursuing their own interests in terms of energy, stability, robustness, and so on. Even if the molecules would not be capable of making the socially optimal decision by themselves, they may be led by the surrounding environment to interact with each other to result in the nearly optimal state of the system. It may be required that such an environment, which would include some parameters of the interactions among the molecules, should not be static and should vary its conditions dynamically depending on the states of the molecules. I imagine that the molecules might obtain a great benefit by constituting such a system under a certain dynamic environment, and it might be one of the reasons why life has emerged in the primordial Earth where diverse environments could be provided.

How could it be possible? This would be a question that is a research subject targeted recently by an emerging field called "systems chemistry", which explores emergent phenomena in complex chemical reaction networks [4]. If we cannot answer this question, we cannot understand the nature of these critically important chemical systems that were put in place to support initial life. There must have been some necessities that triggered the transition from the stage of simple molecular assemblies to the stage of complex molecular networks.

I would like to design a chemical experiment that represents the above-mentioned setting in which the molecules can obtain a great benefit when constituting a system to work as a team, while they reach undesirable equilibrated conditions when making selfish decisions. When the experiment could be successfully designed, I believed that it will produce many clues to understand environmental conditions for the molecules to support the origins of life. If you have any suggestions for how I might design such an experiment, please do share!

References
[1] N. Nisan, T. Roughgarden, E. Tardos, E, V. V. Vazirani (eds.): Algorithmic Game Theory. Cambridge University Press (2007).
[2] T. Roughgarden: Selfish Routing and the Price of Anarchy. The MIT Press (2005).
[3] M. Aono, Y. Hirata, M. Hara, K. Aihara: Greedy versus social: Resource-competing oscillator network as a model of amoeba-based neurocomputer, Natural Computing 10, 1219-1244 (2011).
[4] http://www.jsystchem.com/

Go to Top